Алгоритм Бойера-Мура
Алгоритм Бойера-Мура, разработанный двумя учеными – Бойером (Robert
S. Boyer) и Муром (J. Strother Moore), считается наиболее быстрым среди
алгоритмов общего назначения, предназначенных для поиска подстроки в
строке. Прежде чем рассмотреть работу этого алгоритма, уточним
некоторые термины. Под строкой мы будем понимать всю
последовательность символов текста. Собственно говоря, речь не
обязательно должна идти именно о тексте. В общем случае строка – это
любая последовательность байтов. Поиск подстроки в строке
осуществляется по заданному образцу, т. е. некоторой
последовательности байтов, длина которой не превышает длину строки.
Наша задача заключается в том, чтобы определить, содержит ли строка
заданный образец.
Простейший вариант алгоритма Бойера-Мура состоит из следующих шагов.
На первом шаге мы строим таблицу смещений для искомого образца. Процесс
построения таблицы будет описан ниже. Далее мы совмещаем начало строки
и образца и начинаем проверку с последнего символа образца. Если
последний символ образца и соответствующий ему при наложении символ
строки не совпадают, образец сдвигается относительно строки на
величину, полученную из таблицы смещений, и снова проводится сравнение,
начиная с последнего символа образца. Если же символы совпадают,
производится сравнение предпоследнего символа образца и т. д. Если все
символы образца совпали с наложенными символами строки, значит мы нашли
подстроку и поиск окончен. Если же какой-то (не последний) символ
образца не совпадает с соответствующим символом строки, мы сдвигаем
образец на один символ вправо и снова начинаем проверку с последнего
символа. Весь алгоритм выполняется до тех пор, пока либо не будет
найдено вхождение искомого образца, либо не будет достигнут конец
строки.
Величина сдвига в случае несовпадения последнего символа вычисляется
исходя из следующих соображений: сдвиг образца должен быть минимальным,
таким, чтобы не пропустить вхождение образца в строке. Если данный
символ строки встречается в образце, мы смещаем образец таким образом,
чтобы символ строки совпал с самым правым вхождением этого символа в
образце. Если же образец вообще не содержит этого символа, мы сдвигаем
образец на величину, равную его длине, так что первый символ образца
накладывается на следующий за проверявшимся символ строки.
Величина смещения для каждого символа образца зависит только от
порядка символов в образце, поэтому смещения удобно вычислить заранее и
хранить в виде одномерного массива, где каждому символу алфавита
соответствует смещение относительно последнего символа образца.
Поясним
все вышесказанное на простом примере. Пусть у нас есть набор символов
из пяти символов: a, b, c, d, e и мы хотим найти вхождение образца
“abbad” в строке “abeccacbadbabbad”.
Следующие схемы иллюстрируют этапы выполнения алгоритма
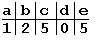
Определяем таблицу смещений для образца “abbad”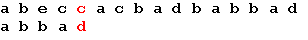
Начало поиска. Последний символ образца не совпадает с наложенным символом строки. Сдвигаем образец вправо на 5 позиций:
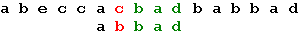
Три символа образца совпали, а четвертый – нет. Сдвигаем образец вправо на одну позицию: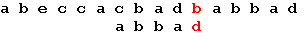 Последний символ снова не совпадает с символом строки. В соответствии с таблицей смещений сдвигаем образец на 2 позиции: Последний символ снова не совпадает с символом строки. В соответствии с таблицей смещений сдвигаем образец на 2 позиции:
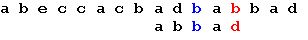 Еще раз сдвигаем образец на 2 позиции: Еще раз сдвигаем образец на 2 позиции: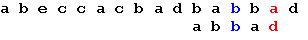 Теперь, в соответствии с таблицей, сдвигаем образец на одну позицию, и получаем искомое вхождение образца: Теперь, в соответствии с таблицей, сдвигаем образец на одну позицию, и получаем искомое вхождение образца:
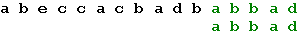
Реализация алгоритма Реализуем указанный алгоритм на языке Pascal (Object). Прежде всего
следует определить тип данных «таблица смещений». Для кодовой таблицы,
состоящей из 256 символов, определение этого типа будет выглядеть так: type
TBMTable = array [0..255] of Integer;
Далее приводится процедура, вычисляющая таблицу смещений для образца P.
procedure MakeBMTable( var BMT : TBMTable; const P : String);
var
i : Integer;
begin
for i := 0 to 255 do BMT[i] := Length(P);
for i := Length(P) downto 1 do
if BMT[Byte(P[i])] = Length(P) then
BMT[Byte(P[i])] := Length(P) – i;
end;
Напишем функцию, осуществляющую поиск
function BMSearch( StartPos : Integer; const S, P : String;
const BMT : TBMTable) : Integer;
var
Pos, lp, i : Integer;
begin
lp := Length(P);
Pos := StartPos + lp –1;
while Pos < Length(S) do
if P[lp] <> S[Pos] then Pos := Pos + BMT[S[Pos]]
else for i := lp - 1 downto 1 do
if P[i] <> S[Pos – lp + i] then
begin
Inc(Pos);
Break;
end
else if i = 1 then
begin
Result := Pos – lp + 1;
Exit;
end;
Result := 0;
end;
Функция BMSearch возвращает позицию первого символа первого
вхождения образца P в строке S. Если последовательность P в S не
найдена, функция возвращает 0 (напомню, что в ObjectPascal нумерация
символов в строке String начинается с 1). Параметр StartPos позволяет
указать позицию в строке S, с которой следует начинать поиск. Это может
быть полезно в том случае, если вы захотите найти все вхождения P в S.
Для поиска с самого начала строки следует задать StartPos равным 1.
Если результат поиска не равен нулю, то для того, чтобы найти следующее
вхождение P в S, нужно задать StartPos равным значению «предыдущий
результат плюс длина образца».
Источник: http://www.rsdn.ru/mag/main.htm | 
